Funciones
A modo de recapitulación, podemos definir función de la siguiente manera:
Una función es una correspondencia entre dos conjuntos A y B no vacíos, en la cual para todo elemento que pertenece al conjunto A existe un solo elemento, y solo uno, que pertenece al conjunto B al cual se le asocia o corresponde.
Para simbolizar que se ha establecido una función f , de un conjunto A en un conjunto B, se usa la siguiente notación:
f : A → B
Criterio de la función
En un sentido abstracto, calcular una función consiste en examinar la correspondencia general de “y” con respecto a “x” , expresado en la fórmula abstracta:
y = f(x)
Esta fórmula establece que la magnitud “y” está, de modo general, en función de “x”.
Ojo, que la magnitud “y” corresponde a lo que luego llamaremos “imagen”, y que depende del valor que se le asigne a “x” (que será la “preimagen”) en f(x).
La notación y = f (x) se lee “y” es una función de “x” o “y” es igual a f de x (esta notación no significa f por (x)). Obviamente en lugar de “x” e “y” hubiésemos podido emplear “variable”, y escribirlo así:
Variable dependiente = f (variable independiente)
Ejemplo 1
Si A = {1, 2, 3} y B = {2, 4, 6} y su correspondencia es el doble.
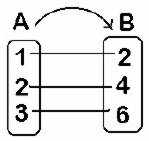
Entonces f(x) = 2x
En efecto
f(1) = 2 • 1 = 2
f(2) = 2 • 2 = 4
f(3) = 2 • 3 = 6
Tenemos
Dominio = {1, 2, 3}
Codominio = {2, 4, 6}
Ámbito (rango o recorrido) = {2, 4, 6}
Ejemplo 2
Si A = {1, 3, 5} y B = {3, 5, 7, 9, 11} y su correspondencia es el doble más uno.
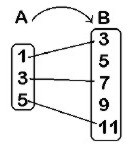
Entonces f(x) = 2x + 1
En efecto:
f(1) = 2 • 1 + 1 = 3
f(3) = 2 • 3 + 1 = 7
f(5) = 2 • 5 + 1 = 11
Tenemos
Dominio = {1, 3, 5}
Codominio = {3, 5, 7, 9, 11}
Ámbito (rango o recorrido) = {3, 7, 11}
Conceptos básicos de la función
Conceptos básicos de la función
Dada una función f : A → B (es lo mismo que f : X → Y ) se define:
* El conjunto A se llama conjunto de partida o dominio , se puede representar como f D.
* Al conjunto B se llama conjunto de llegada o codominio .
* Se llaman preimágenes a los elementos del conjunto de partida o dominio.
* Se llaman imágenes a los elementos del conjunto de llegada o codominio que están asociados a una preimagen, mediante el criterio de la función.
* Se llama rango (recorrido o ámbito) de una función al conjunto formado por las imágenes. Este conjunto es un subconjunto del codominio, se puede representar como f R ó f A, respectivamente.
Para ilustrar los conceptos anteriores usaremos lo que se denomina Diagramas de Venn-Euler.
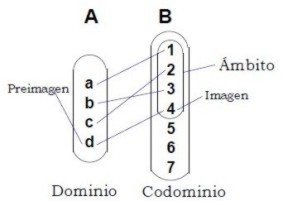
Ejemplo 3
Analizar el siguiente diagrama que representa una función y determinar el dominio, codominio y el ámbito (rango o recorrido).
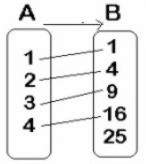
Tenemos
Dominio (Df) = {1, 2, 3, 4}
Codominio = {1, 4, 9, 16, 25}
Ámbito (Af) = {1, 4, 9, 16}
Ejemplo 4
Analizar el siguiente diagrama que representa una función y determinar el dominio, codominio y el ámbito.
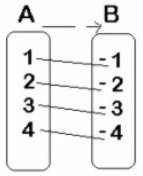
Tenemos
Dominio (Df) = {1,2 3, 4}
Codominio = {−1, −2, −3, −4}
Ámbito (Af) = {−1, −2, −3, −4}
Recuerda que los elementos del dominio se llaman preimágenes y los
elementos del ámbito (rango o recorrido) se llaman imágenes.
elementos del ámbito (rango o recorrido) se llaman imágenes.
Debido a que es posible que el codominio y el ámbito estén compuestos por el mismo conjunto de elementos, suele pensarse que codominio y ámbito es lo mismo, el concepto y los ejemplos anteriores nos permiten darnos cuenta que pensar así es un error.
Cálculo de la imagen
Debemos recordar que el conjunto de partida esta formado por las preimágenes y, se llama dominio , las preimágenes son los valores que toma la variable independiente .
Ejemplo 5
Un carpintero gasta $350 por cada silla que haga más un monto fijo de $2.000 por día ¿cuánto gastará si hace 2 sillas por día? ¿Cuánto gastará si hace 4, 6 u 8 sillas por día?
Para este ejemplo, x representa cada silla y f(x) el costo de fabricarla, lo cual significa que el costo es igual a multiplicar 350 por cada silla y sumarle el gasto fijo. Es decir:
f(x) = 350x + 2.000
Por lo que el valor de la variable independiente x para la primera pregunta es 2. Para encontrar la respuesta sustituimos el valor de dicha variable en el criterio de la función.
f(2) = 350 • 2 + 2.000
f(2) = 700 + 2.000
f(2) = 2.700
Entonces si hace solamente 2 sillas en un día, gastaría $2.700 en hacerlas.
De esto podemos decir que 2 es la preimagen de 2.700.
De esto podemos decir que 2 es la preimagen de 2.700.
Además:
f(4) = 350 • 4 + 2.000 = 3.400
f(6) = 350 • 6 + 2.000 = 4.100
f(8) = 350 • 8 + 2.000 = 4.800
Tenemos, entonces:
fD = {2, 4, 6, 8}
Codominio: {2.700, 3.400, 4.100, 4.800}
Ejemplo 6
Tenemos f(x)= x 2 – 6x +7 ¿Cuál es la imagen de 10?
Dado que nos preguntan por la imagen esto significa que 10 es una preimagen por lo que x = 10
f(10) = 10 2 − 6 • 10 + 7
f(10) = 100 − 60 + 7
f(10) = 47
Cálculo de la preimagen
Para calcular la preimagen de una función, conociendo la imagen y el criterio (el miembro de la derecha de la ecuación), se iguala el criterio de la función con la imagen que se tiene.
Despejando la incógnita de la ecuación que se forma se determina el valor de la variable.
Ejemplo 7
Si tenemos f(x)= x 2 – 6 ¿Cuál es la preimagen de – 5 ?
Dado que nos preguntan por la preimagen esto significa que –5 es una imagen por lo que f(x) = –5
−5 = x 2 – 6
− 5 + 6 = x 2
1 = x 2
x = ± 1
Las preimágenes de –5 son –1 y 1. Para este caso recordemos que en una función una imagen debe tener al menos una preimagen, aunque puede tener más de una.
Ejemplo 8
Si tenemos f(x)= 3x + 5 ¿Cuál es la preimagen de 11?
Dado que nos preguntan por la preimagen esto significa que 11 es una imagen por lo que f(x) = 11
11 = 3x + 5
11 − 5 = 3x
6 = 3x
2 = x
La preimagen de 11 es 2.
