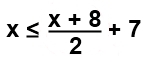¿A qué edad hay que casarse?

En la sociedad india existe la creencia de que para que una relación sentimental tenga futuro la edad de la mujer no debe superar la mitad más siete de la edad del varón.
Si un caballero indio tuviera 8 años más que la mujer, ¿hasta qué edad puede ella formalizar su relación?
¿Cómo se expresan matemáticamente las condiciones planteadas en esta situación?
1) Seleccionamos la letra X para representar la edad de la mujer, ya que todos los datos están en función de ella. edad de la mujer→ X 2) El varón tiene 8 años más que la mujer. edad del varón →X + 8 3) Además, la edad de la mujer no debe superar (debe ser menor o igual) la mitad más siete de la edad del varón. 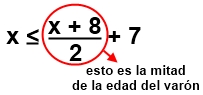
A este tipo de desigualdades se le llama INECUACIONES.
En este recurso veremos qué son las inecuaciones y cómo se resuelven

En la sociedad india existe la creencia de que para que una relación sentimental tenga futuro la edad de la mujer no debe superar la mitad más siete de la edad del varón.
Si un caballero indio tuviera 8 años más que la mujer, ¿hasta qué edad puede ella formalizar su relación?
¿Cómo se expresan matemáticamente las condiciones planteadas en esta situación?
| 1) Seleccionamos la letra X para representar la edad de la mujer, ya que todos los datos están en función de ella. | edad de la mujer→ X |
| 2) El varón tiene 8 años más que la mujer. | edad del varón →X + 8 |
| 3) Además, la edad de la mujer no debe superar (debe ser menor o igual) la mitad más siete de la edad del varón. |  |
A este tipo de desigualdades se le llama INECUACIONES.
En este recurso veremos qué son las inecuaciones y cómo se resuelven
Una desigualdad es cualquier expresión en la que se utilicen alguno de los siguientes símbolos:
< (menor que),
> (mayor que)
≤ (menor o igual que)
≥ (mayor o igual que)
> (mayor que)
≤ (menor o igual que)
≥ (mayor o igual que)
Por ejemplo:
2 < 3 (dos es menor que 3)
7 > (siete es mayor que pi)
(siete es mayor que pi)
x ≤ 5 (x es menor o igual que 5)
7 >
 (siete es mayor que pi)
(siete es mayor que pi)x ≤ 5 (x es menor o igual que 5)
| Una inecuación es una desigualdad entre expresiones algebraicas. |
Ejemplos:
| 3x + 7y < 5 | Los números o las expresiones que aparecen a ambos lados de los símbolos de la desigualdad reciben el nombre de miembrosde la desigualdad. |
x2 - 3x + 5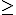 0 0 | |
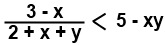 |
Comencemos por las más sencillas, por ejemplo:
x > -2 a las que llamaremos de "resolución inmediata"
De manera similar que en las ecuaciones:
Resolver una inecuación es hallar los valores de la incógnita que la transforman en una desigualdad numérica.

Son todos los números mayores que -2.
Si trabajamos en R el conjunto solución es S = {x 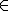 R / x > -2}
R / x > -2}
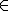 R / x > -2}
R / x > -2}
En forma gráfica:

Tomemos ahora el ejemplo x + 5 > -3
Para este tipo de inecuaciones, y otras que no sean de resolución inmediata, veremos si son posibles las transformaciones que has estudiado para las ecuaciones.
Como la X representa números, no estamos hablando de otra cosa que de desigualdades entre números.
 ¿Qué sucede si sumamos a ambos miembros de una desigualdad un mismo número?
¿Qué sucede si sumamos a ambos miembros de una desigualdad un mismo número?| Por ejemplo | 7 > -5 | ||
| sumando -8 a ambos miembros | 7 -8 ? -5 -8 | ||
| obtenemos | -1 > -13 | ||
| o sea otra desigualdad del mismo sentido |
| Si se suma a ambos miembros de una inecuación una misma expresión entera obtenemos otra inecuación equivalente. |
Por lo tanto para resolver la inecuación planteada al inicio haremos:
x + 5 > -3
x + 5 - 5 > - 3 - 5
x > - 3 - 5
x > -8
S = {xR / x > -8}
¿Qué sucede si multiplicamos ambos miembros de una desigualdad por un mismo número distinto de 0?
| Veamos: | -4 < 3 |
| Multiplicando por 5 será | -4 . 5 ? 3 . 5 |
| -20 < 15 | |
| ¿y si multiplicamos por 1/2? | -4 < 1 |
| -4 . 1/2 ? 1 . 1/2 | |
| -2 < 1/2 |

¿Y si multiplicamos por un número negativo?
7 > 3
-3 . 7 ? -3 . 3
-21 < -9
Observa entonces que, al multiplicar ambos miembros por un mismo número distinto de 0, se obtiene otra desigualdad del mismo sentido EXCEPTO CUANDO EL NÚMERO ES NEGATIVO.
| Si se multiplican ambos miembros de una inecuación por un mismo número distinto de 0 se obtiene una inecuación equivalente, teniendo en cuenta que si el número es negativo la inecuación cambia de sentido. |
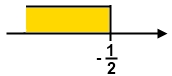
Por lo tanto para resolver 4x 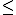 -2 haremos:
-2 haremos:
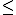 -2 haremos:
-2 haremos: 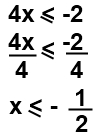
S = {xR / x < - 1/2}
Y para resolver -3x > -1 haremos: 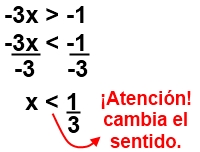

S = {x  R / x < 1/3}
R / x < 1/3}
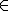 R / x < 1/3}
R / x < 1/3}

Ahora que ya sabes resolver inecuaciones puedes contestar la pregunta planteada al inicio de este recurso:En la sociedad india existe la creencia de que para que una relación sentimental tenga futuro la edad de la mujer no debe superar la mitad más siete de la edad del varón.Si un caballero indio tuviera 8 años más que la mujer, ¿hasta qué edad puede ella formalizar su relación?